NLP自然语言处理相关技术说明及样例(附源码)
1、简单概述
1.1 NLP概念
NLP(Natural Language Processing),自然语言处理,又称NLU(Natural Language Understanding)自然语言理解,是语言信息处理的分支,也是人工智能的核心课题,简单来说就是让计算机理解自然语言。
1.2 NLP涉及的内容及技术
自然语言处理研究包含的内容十分广泛,这里只列举出其中的其中的一部分(主要是在移动易系统中涉及到的),包括分词处理(Word-Segment),词性标注(Part-of-Speech tagging),句法分析(Parsing),信息检索(Infomation-Retrieval),文字校对(Text-Rroofing),词向量模型(WordVector-Model),语言模型(Language-Model),问答系统(Question-Answer-System)。如下逐一介绍。
2、前期准备
- Lucene使用经验
- python使用经验
- 相关工具包如下:
| 工具 | 版本 | 下载地址 |
|---|---|---|
| 哈工大LTP | ltp4j | download |
| berkeleylm | berkeleylm 1.1.5 | download |
| ElasticSearch | elasticsearch-2.4.5 | download |
3、具体实现
3.1 分词(Word-Segment)
3.1.1 这里主要介绍中文分词的实现,实现中文分词的方法有许多种,例如StandfordCore NLP(具体实现参见【NLP】使用 Stanford NLP 进行中文分词 ),jieba分词,这里使用哈工大的语言技术平台LTP(包括后面的词性标注,句法分析)。具体步骤如下:
- 首先下载LTP4J的jar包(download),
- 下载完解压缩后的文件包为ltp4j-master,相应的jar包就在output文件夹下的jar文件夹中。
- 下载编译好的C++动态链接库download,解压后如下所示:
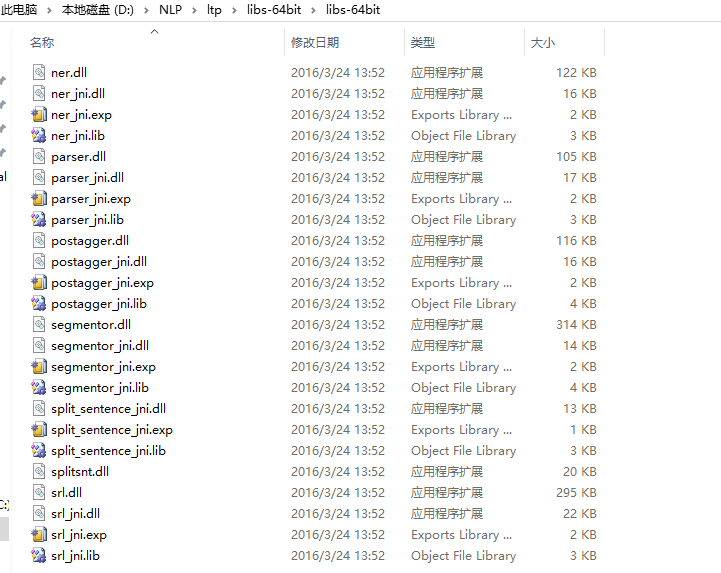
- 将文件夹中的所有内容复制到jdk的bin目录下,如下所示:
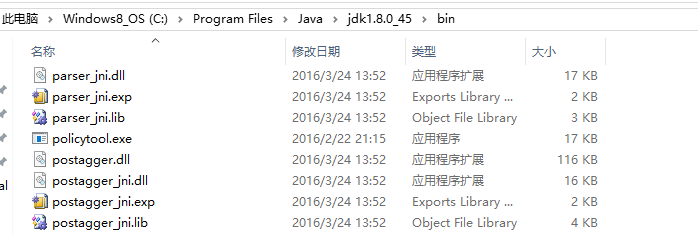
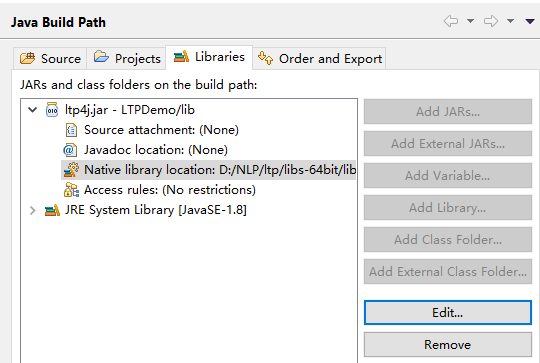
- 构建Java项目,将jar包导入到项目中,右键项目buildpath,为添加的jar包添加本来地库依赖,路劲即下载解压后的dll动态库文件路径,如下所示:
- 接着便是中文分词的测试了,实现代码如下:
package ccw.ltpdemo;
import java.util.ArrayList;
import java.util.List;
import edu.hit.ir.ltp4j.Segmentor;
public class ltpSegmentDemo {
public static void main(String[] args) {
Segmentor segmentor = new Segmentor();
if(segmentor.create("D:/NLP/ltp/ltp_data_v3.4.0/ltp_data_v3.4.0/cws.model")<0)
{
System.out.println("model load failed");
}
else
{
String sent = "这是中文分词测试";
List<String> words = new ArrayList<String>();
int size = segmentor.segment(sent, words);
for(String word :words)
{
System.out.print(word+"\t");
}
segmentor.release();
}
}
}3.1.2 效果如下:
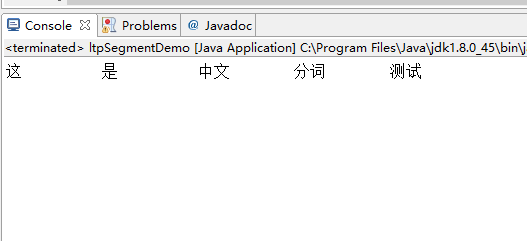
3.2 词性标注(Part-of-Speech tagging)
3.2.1 这里介绍如何通过ltp实现中文的词性标注,具体实现代码如下:
package ccw.ltpdemo;
import java.util.ArrayList;
import java.util.List;
import edu.hit.ir.ltp4j.Postagger;
public class ltpPostaggerDemo {
public static void main(String[] args) {
Postagger postagger = new Postagger();
if(postagger.create("D:/NLP/ltp/ltp_data_v3.4.0/ltp_data_v3.4.0/pos.model")<0)
{
System.out.println("model load failed");
}
else
{
List<String> words = new ArrayList<String>();
words.add("我");
words.add("是");
words.add("中国");
words.add("人");
List<String> values = new ArrayList<String>();
int size = postagger.postag(words, values);
for(int i = 0;i<words.size();i++)
{
System.out.print(words.get(i)+" "+values.get(i)+"\t");
}
postagger.release();
}
}
}
3.2.2 实现效果如下:
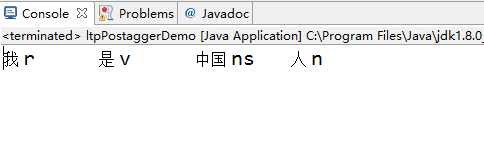
3.3 句法分析(Parsing)
3.3.1 这里介绍如何通过ltp实现对中文句子的句法分析,核心方法int size = Parser.parse(words,tags,heads,deprels),其中,words[]表示待分析的词序列,tags[]表示待分析的词的词性序列,heads[]表示结果依存弧,heads[i]代表第i个节点的父节点编号(其中第0个表示根节点root),deprels[]表示依存弧的关系类型,size表示返回结果中词的个数。实现代码如下:
package ccw.ltpdemo;
import java.util.ArrayList;
import java.util.List;
import edu.hit.ir.ltp4j.Parser;
public class ltpParserDemo {
/**
* @param args
*/
public static void main(String[] args) {
Parser parser = new Parser();
if(parser.create("D:/NLP/ltp/ltp_data_v3.4.0/ltp_data_v3.4.0/parser.model")<0)
{
System.out.println("model load failed");
}
else
{
List<String> words = new ArrayList<String>();
List<String> tags = new ArrayList<String>();
words.add("我");tags.add("r");
words.add("非常");tags.add("d");
words.add("喜欢");tags.add("v");
words.add("音乐");tags.add("n");
List<Integer> heads = new ArrayList<Integer>();
List<String> deprels = new ArrayList<String>();
int size = Parser.parse(words,tags,heads,deprels);
for(int i = 0;i<size;i++) {
System.out.print(heads.get(i)+":"+deprels.get(i));
if(i==size-1) {
System.out.println();
}
else{
System.out.print(" ");
}
}
parser.release();
}
}
}
3.3.2 实现效果如下:
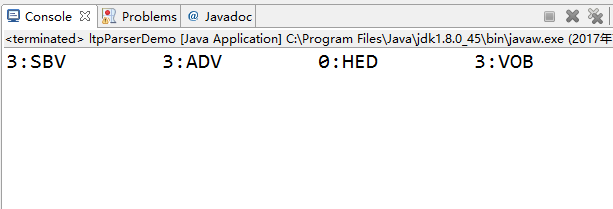
3.4 信息检索(Information-Retrieval)
信息检索(Information Retrieval)是用户进行信息查询和获取的主要方式,是查找信息的方法和手段。狭义的信息检索仅指信息查询(Information Search)。即用户根据需要,采用一定的方法,借助检索工具,从信息集合中找出所需要信息的查找过程。实现参见移动易实现全文搜索。
3.5 文字校对(Text-Rroofing),语言模型(Language-Model)
3.5.1 N元模型(N-gram)
首先介绍N-gram模型,N-gram模型是自然语言处理中一个非常重要的概念,通常,在NLP中,基于一定的语料库, 可以通过N-gram来预计或者评估一个句子是否合理。对于一个句子T,假设T由词序列w1,w2,w3...wn组成,那么T出现的概率
- P(T)=P(w1,w2,w3...wn)=P(w1)P(w2|w1)P(w3|w2,w1)...p(wn|wn-1,...w2,w1),
此概率在参数巨大的情况下显然不容易计算,因此引入了马尔可夫链(即每个词出现的概率仅仅与它的前后几个词相关),这样可以大幅度缩小计算的长度,即 - P(wi|w1,⋯,wi−1)=P(wi|wi−n+1,⋯,wi−1)
特别的,当n取值较小时:
当n=1时,即每一个词出现的概率只由该词的词频决定,称为一元模型(unigram-model): - P(w1,w2,⋯,wm)=∏i=1mP(wi)
设M表示语料库中的总字数,c(wi)表示wi在语料库中出现的次数,那么 - P(wi)=C(wi)/M
当n=2时,即每一个词出现的概率只由该词的前一个词以及后一个词决定,称为二元模型(bigram-model): - P(w1,w2,⋯,wm)=∏i=1mP(wi|wi−1)
设M表示语料库中的总字数,c(wi-1WI)表示wi-1wi在语料库中出现的次数,那么 - P(wi|wi−1)=C(wi−1wi)/C(wi−1)
当n=3时,称为三元模型(trigram-model): - P(w1,w2,⋯,wm)=∏i=1mP(wi|wi−2wi−1)
那么 - P(wi|wi−1wi-2)=C(wi-2wi−1wi)/C(wi−2wi-1)
3.5.2 中文拼写纠错
接着介绍如何通过Lucene提供的spellChecker(拼写校正)模块实现中文字词的纠错,首先创建语料词库,如下所示:
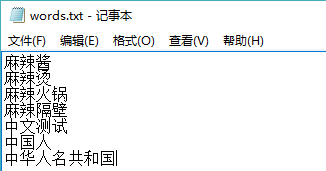
然后在代码中创建索引并测试,具体实现代码如下:
package ccw.spring.ccw.lucencedemo;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Iterator;
import org.apache.lucene.index.IndexReader;
import org.apache.lucene.index.IndexWriterConfig;
import org.apache.lucene.search.spell.LuceneDictionary;
import org.apache.lucene.search.spell.PlainTextDictionary;
import org.apache.lucene.search.spell.SpellChecker;
import org.apache.lucene.search.suggest.InputIterator;
import org.apache.lucene.store.Directory;
import org.apache.lucene.store.FSDirectory;
import org.apache.lucene.util.Version;
public class Spellcheck {
public static String directorypath;
public static String origindirectorypath;
public SpellChecker spellcheck;
public LuceneDictionary dict;
/**
* 创建索引
* a
* @return
* @throws IOException
* boolean
*/
public static void createIndex(String directorypath,String origindirectorypath) throws IOException
{
Directory directory = FSDirectory.open(new File(directorypath));
SpellChecker spellchecker = new SpellChecker(directory);
IndexWriterConfig config = new IndexWriterConfig(Version.LUCENE_4_9, null);
PlainTextDictionary pdic = new PlainTextDictionary(new InputStreamReader(new FileInputStream(new File(origindirectorypath)),"utf-8"));
spellchecker.indexDictionary(new PlainTextDictionary(new File(origindirectorypath)), config, false);
directory.close();
spellchecker.close();
}
public Spellcheck(String opath ,String path)
{
origindirectorypath = opath;
directorypath = path;
Directory directory;
try {
directory = FSDirectory.open(new File(directorypath));
spellcheck = new SpellChecker(directory);
IndexReader oriIndex = IndexReader.open(directory);
dict = new LuceneDictionary(oriIndex,"name");
}
catch (IOException e) {
e.printStackTrace();
}
}
public void setAccuracy(float v)
{
spellcheck.setAccuracy(v);
}
public String[]search(String queryString, int suggestionsNumber)
{
String[]suggestions = null;
try {
if (exist(queryString))
return null;
suggestions = spellcheck.suggestSimilar(queryString,suggestionsNumber);
}
catch (IOException e)
{
e.printStackTrace();
}
return suggestions;
}
private boolean exist(String queryString) throws IOException {
InputIterator ite = dict.getEntryIterator();
while (ite.hasContexts())
{
if (ite.next().equals(queryString))
return true;
}
return false;
}
public static void main(String[] args) throws IOException {
String opath = "D:\\Lucene\\NLPLucene\\words.txt";
String ipath = "D:\\Lucene\\NLPLucene\\index";
Spellcheck.createIndex(ipath, opath);
Spellcheck spellcheck = new Spellcheck(opath,ipath);
//spellcheck.createSpellIndex();
spellcheck.setAccuracy((float) 0.5);
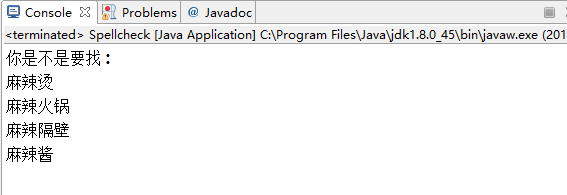
String [] result = spellcheck.search("麻辣糖", 15);
if(result.length==0||null==result)
{
System.out.println("未发现错误");
}
else
{
System.out.println("你是不是要找:");
for(String hit:result)
{
System.out.println(hit);
}
}
}
}
实现效果如下:
3.5.3 中文语言模型训练
这里主要介绍中文语言模型的训练,中文语言模型的训练主要基于N-gram算法,目前开源的语言模型训练的工具主要有SRILM、KenLM、 berkeleylm 等几种,KenLm较SRILM性能上要好一些,用C++编写,支持单机大数据的训练。berkeleylm是用java写。本文主要介绍如何通过berkelylm实现中文语言模型的训练。
- 首先需要下载berkeleylm的jar包(download),完成后将jar包导入到java项目中。
- 然后准备训练的语料库,首先通过ltp将每一句文本分词,然后将分完词的语句写入txt文件,如下所示:

- 接着就是对语料库的训练,首先要读取分完词的文本,然后就是对每个词计算在给定上下文中出现的概率,这里的概率是对10取对数后计算得到的,最后将结果按照给定的格式存储,可以按照.arpa或者二进制.bin文件存储。文件格式如下:

实现代码如下:
package ccw.berkeleylm;
import java.io.File;
import java.util.ArrayList;
import java.util.List;
import edu.berkeley.nlp.lm.ConfigOptions;
import edu.berkeley.nlp.lm.StringWordIndexer;
import edu.berkeley.nlp.lm.io.ArpaLmReader;
import edu.berkeley.nlp.lm.io.LmReaders;
import edu.berkeley.nlp.lm.util.Logger;
public class demo {
private static void usage() {
System.err.println("Usage: <lmOrder> <ARPA lm output file> <textfiles>*");
System.exit(1);
}
public void makelml(String [] argv)
{
if (argv.length < 2) {
usage();
}
final int lmOrder = Integer.parseInt(argv[0]);
final String outputFile = argv[1];
final List<String> inputFiles = new ArrayList<String>();
for (int i = 2; i < argv.length; ++i) {
inputFiles.add(argv[i]);
}
if (inputFiles.isEmpty()) inputFiles.add("-");
Logger.setGlobalLogger(new Logger.SystemLogger(System.out, System.err));
Logger.startTrack("Reading text files " + inputFiles + " and writing to file " + outputFile);
final StringWordIndexer wordIndexer = new StringWordIndexer();
wordIndexer.setStartSymbol(ArpaLmReader.START_SYMBOL);
wordIndexer.setEndSymbol(ArpaLmReader.END_SYMBOL);
wordIndexer.setUnkSymbol(ArpaLmReader.UNK_SYMBOL);
LmReaders.createKneserNeyLmFromTextFiles(inputFiles, wordIndexer, lmOrder, new File(outputFile), new ConfigOptions());
Logger.endTrack();
}
public static void main(String[] args) {
demo d = new demo();
String inputfile = "D:\\NLP\\languagematerial\\quest.txt";
String outputfile = "D:\\NLP\\languagematerial\\q.arpa";
String s[]={"8",outputfile,inputfile};
d.makelml(s);
}
}
- 最后就是读取模型,然后判断句子的相似性,实现代码如下:
package ccw.berkeleylm;
import java.io.File;
import java.util.ArrayList;
import java.util.List;
import edu.berkeley.nlp.lm.ArrayEncodedProbBackoffLm;
import edu.berkeley.nlp.lm.ConfigOptions;
import edu.berkeley.nlp.lm.StringWordIndexer;
import edu.berkeley.nlp.lm.io.LmReaders;
public class readdemo {
public static ArrayEncodedProbBackoffLm<String> getLm(boolean compress,String file) {
final File lmFile = new File(file);
final ConfigOptions configOptions = new ConfigOptions();
configOptions.unknownWordLogProb = 0.0f;
final ArrayEncodedProbBackoffLm<String> lm = LmReaders.readArrayEncodedLmFromArpa(lmFile.getPath(), compress, new StringWordIndexer(), configOptions,
Integer.MAX_VALUE);
return lm;
}
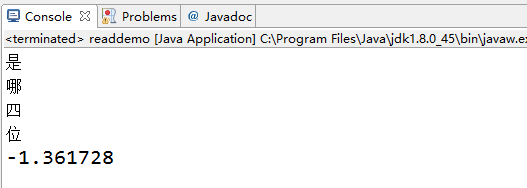
public static void main(String[] args) {
readdemo read = new readdemo();
LmReaders readers = new LmReaders();
ArrayEncodedProbBackoffLm<String> model = (ArrayEncodedProbBackoffLm) readdemo.getLm(false, "D:\\NLP\\languagematerial\\q.arpa");
String sentence = "是";
String [] words = sentence.split(" ");
List<String> list = new ArrayList<String>();
for(String word : words)
{
System.out.println(word);
list.add(word);
}
float score = model.getLogProb(list);
System.out.println(score);
}
}
实现效果如下:
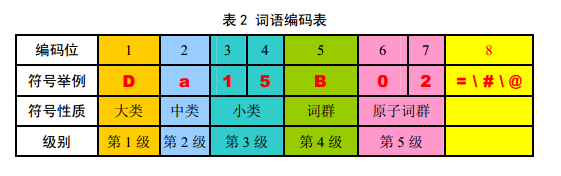
3.5.4 同义词词林
这里使用哈工大提供的同义词词林,词林提供三层编码,第一级大类用大写英文字母表示,第二级中类用小写字母表示,第三级小类用二位十进制整数表示,第四级词群用大写英文字母表示,第五级原子词群用二位十进制整数表示。编码表如下所示:
第八位的标记有三种,分别是“=“、”#“、”@“,=代表相等、同义,#代表不等、同类,@代表自我封闭、独立,它在词典中既没有同义词,也没有相关词。通过同义词词林可以比较两词的相似程度,代码实现如下:
package cilin;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.HashMap;
import java.util.List;
import java.util.Vector;
public class CiLin {
public static HashMap<String, List<String>> keyWord_Identifier_HashMap;//<关键词,编号List集合>哈希
public int zero_KeyWord_Depth = 12;
public static HashMap<String, Integer> first_KeyWord_Depth_HashMap;//<第一层编号,深度>哈希
public static HashMap<String, Integer> second_KeyWord_Depth_HashMap;//<前二层编号,深度>哈希
public static HashMap<String, Integer> third_KeyWord_Depth_HashMap;//<前三层编号,深度>哈希
public static HashMap<String, Integer> fourth_KeyWord_Depth_HashMap;//<前四层编号,深度>哈希
//public HashMap<String, HashSet<String>> ciLin_Sort_keyWord_HashMap = new HashMap<String, HashSet<String>>();//<(同义词)编号,关键词Set集合>哈希
static{
keyWord_Identifier_HashMap = new HashMap<String, List<String>>();
first_KeyWord_Depth_HashMap = new HashMap<String, Integer>();
second_KeyWord_Depth_HashMap = new HashMap<String, Integer>();
third_KeyWord_Depth_HashMap = new HashMap<String, Integer>();
fourth_KeyWord_Depth_HashMap = new HashMap<String, Integer>();
initCiLin();
}
//3.初始化词林相关
public static void initCiLin(){
int i;
String str = null;
String[] strs = null;
List<String> list = null;
BufferedReader inFile = null;
try {
//初始化<关键词, 编号set>哈希
inFile = new BufferedReader(new InputStreamReader(new FileInputStream("cilin/keyWord_Identifier_HashMap.txt"), "utf-8"));// 读取文本
while((str = inFile.readLine()) != null){
strs = str.split(" ");
list = new Vector<String>();
for (i = 1; i < strs.length; i++)
list.add(strs[i]);
keyWord_Identifier_HashMap.put(strs[0], list);
}
//初始化<第一层编号,高度>哈希
inFile.close();
inFile = new BufferedReader(new InputStreamReader(new FileInputStream("cilin/first_KeyWord_Depth_HashMap.txt"), "utf-8"));// 读取文本
while ((str = inFile.readLine()) != null){
strs = str.split(" ");
first_KeyWord_Depth_HashMap.put(strs[0], Integer.valueOf(strs[1]));
}
//初始化<前二层编号,高度>哈希
inFile.close();
inFile = new BufferedReader(new InputStreamReader(new FileInputStream("cilin/second_KeyWord_Depth_HashMap.txt"), "utf-8"));// 读取文本
while ((str = inFile.readLine()) != null){
strs = str.split(" ");
second_KeyWord_Depth_HashMap.put(strs[0], Integer.valueOf(strs[1]));
}
//初始化<前三层编号,高度>哈希
inFile.close();
inFile = new BufferedReader(new InputStreamReader(new FileInputStream("cilin/third_KeyWord_Depth_HashMap.txt"), "utf-8"));// 读取文本
while ((str = inFile.readLine()) != null){
strs = str.split(" ");
third_KeyWord_Depth_HashMap.put(strs[0], Integer.valueOf(strs[1]));
}
//初始化<前四层编号,高度>哈希
inFile.close();
inFile = new BufferedReader(new InputStreamReader(new FileInputStream("cilin/fourth_KeyWord_Depth_HashMap.txt"), "utf-8"));// 读取文本
while ((str = inFile.readLine()) != null){
strs = str.split(" ");
fourth_KeyWord_Depth_HashMap.put(strs[0], Integer.valueOf(strs[1]));
}
inFile.close();
} catch (Exception e) {
e.printStackTrace();
}
}
//根据两个关键词计算相似度
public static double calcWordsSimilarity(String key1, String key2){
List<String> identifierList1 = null, identifierList2 = null;//词林编号list
if(key1.equals(key2))
return 1.0;
if (!keyWord_Identifier_HashMap.containsKey(key1) || !keyWord_Identifier_HashMap.containsKey(key2)) {//其中有一个不在词林中,则返回相似度为0.1
//System.out.println(key1 + " " + key2 + "有一个不在同义词词林中!");
return 0.1;
}
identifierList1 = keyWord_Identifier_HashMap.get(key1);//取得第一个词的编号集合
identifierList2 = keyWord_Identifier_HashMap.get(key2);//取得第二个词的编号集合
return getMaxIdentifierSimilarity(identifierList1, identifierList2);
}
public static double getMaxIdentifierSimilarity(List<String> identifierList1, List<String> identifierList2){
int i, j;
double maxSimilarity = 0, similarity = 0;
for(i = 0; i < identifierList1.size(); i++){
j = 0;
while(j < identifierList2.size()){
similarity = getIdentifierSimilarity(identifierList1.get(i), identifierList2.get(j));
System.out.println(identifierList1.get(i) + " " + identifierList2.get(j) + " " + similarity);
if(similarity > maxSimilarity)
maxSimilarity = similarity;
if(maxSimilarity == 1.0)
return maxSimilarity;
j++;
}
}
return maxSimilarity;
}
public static double getIdentifierSimilarity(String identifier1, String identifier2){
int n = 0, k = 0;//n是分支层的节点总数, k是两个分支间的距离.
//double a = 0.5, b = 0.6, c = 0.7, d = 0.96;
double a = 0.65, b = 0.8, c = 0.9, d = 0.96;
if(identifier1.equals(identifier2)){//在第五层相等
if(identifier1.substring(7).equals("="))
return 1.0;
else
return 0.5;
}
else if(identifier1.substring(0, 5).equals(identifier2.substring(0, 5))){//在第四层相等 Da13A01=
n = fourth_KeyWord_Depth_HashMap.get(identifier1.substring(0, 5));
k = Integer.valueOf(identifier1.substring(5, 7)) - Integer.valueOf(identifier2.substring(5, 7));
if(k < 0) k = -k;
return Math.cos(n * Math.PI / 180) * ((double)(n - k + 1) / n) * d;
}
else if(identifier1.substring(0, 4).equals(identifier2.substring(0, 4))){//在第三层相等 Da13A01=
n = third_KeyWord_Depth_HashMap.get(identifier1.substring(0, 4));
k = identifier1.substring(4, 5).charAt(0) - identifier2.substring(4, 5).charAt(0);
if(k < 0) k = -k;
return Math.cos(n * Math.PI / 180) * ((double)(n - k + 1) / n) * c;
}
else if(identifier1.substring(0, 2).equals(identifier2.substring(0, 2))){//在第二层相等
n = second_KeyWord_Depth_HashMap.get(identifier1.substring(0, 2));
k = Integer.valueOf(identifier1.substring(2, 4)) - Integer.valueOf(identifier2.substring(2, 4));
if(k < 0) k = -k;
return Math.cos(n * Math.PI / 180) * ((double)(n - k + 1) / n) * b;
}
else if(identifier1.substring(0, 1).equals(identifier2.substring(0, 1))){//在第一层相等
n = first_KeyWord_Depth_HashMap.get(identifier1.substring(0, 1));
k = identifier1.substring(1, 2).charAt(0) - identifier2.substring(1, 2).charAt(0);
if(k < 0) k = -k;
return Math.cos(n * Math.PI / 180) * ((double)(n - k + 1) / n) * a;
}
return 0.1;
}
}
//测试
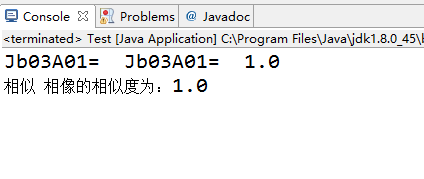
public class Test {
public static void main(String args[]) {
String word1 = "相似", word2 = "相像";
double sim = 0;
sim = CiLin.calcWordsSimilarity(word1, word2);//计算两个词的相似度
System.out.println(word1 + " " + word2 + "的相似度为:" + sim);
}
}
测试效果如下:
3.6 词向量模型(WordVector-Model)
3.6.1 词向量
词向量顾名思义,就是用一个向量的形式表示一个词。为什么这么做?自然语言理解问题转化为机器学习问题的第一步都是通过一种方法把这些符号数学化。词向量具有良好的语义特性,是表示词语特征的常用方式。词向量的每一维的值代表一个具有一定的语义和语法上解释的特征。
3.6.2 Word2vec
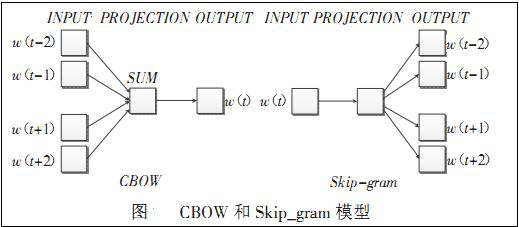
Word2vec是Google公司在2013年开放的一款用于训练词向量的软件工具。它根据给定的语料库,通过优化后的训练模型快速有效的将一个词语表达成向量形式,其核心架构包括CBOW和Skip-gram。Word2vec包含两种训练模型,分别是CBOW和Skip_gram(输入层、发射层、输出层),如下图所示:
3.6.3 word2vec 训练词向量
# coding:utf-8
import sys
reload(sys)
sys.setdefaultencoding( "utf-8" )
from gensim.models import Word2Vec
import logging,gensim,os
class TextLoader(object):
def __init__(self):
pass
def __iter__(self):
input = open('corpus-seg.txt','r')
line = str(input.readline())
counter = 0
while line!=None and len(line) > 4:
#print line
segments = line.split(' ')
yield segments
line = str(input.readline())
sentences = TextLoader()
model = gensim.models.Word2Vec(sentences, workers=8)
model.save('word2vector2.model')
print 'ok'
# coding:utf-8
import sys
reload(sys)
sys.setdefaultencoding( "utf-8" )
from gensim.models import Word2Vec
import logging,gensim,os
#模型的加载
model = Word2Vec.load('word2vector.model')
#比较两个词语的相似度,越高越好
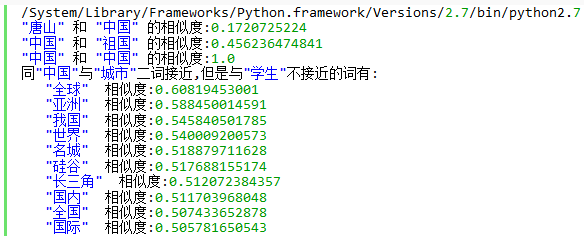
print('"唐山" 和 "中国" 的相似度:'+ str(model.similarity('唐山','中国')))
print('"中国" 和 "祖国" 的相似度:'+ str(model.similarity('祖国','中国')))
print('"中国" 和 "中国" 的相似度:'+ str(model.similarity('中国','中国')))
#使用一些词语来限定,分为正向和负向的
result = model.most_similar(positive=['中国', '城市'], negative=['学生'])
print('同"中国"与"城市"二词接近,但是与"学生"不接近的词有:')
for item in result:
print(' "'+item[0]+'" 相似度:'+str(item[1]))
result = model.most_similar(positive=['男人','权利'], negative=['女人'])
print('同"男人"和"权利"接近,但是与"女人"不接近的词有:')
for item in result:
print(' "'+item[0]+'" 相似度:'+str(item[1]))
result = model.most_similar(positive=['女人','法律'], negative=['男人'])
print('同"女人"和"法律"接近,但是与"男人"不接近的词有:')
for item in result:
print(' "'+item[0]+'" 相似度:'+str(item[1]))
#从一堆词里面找到不匹配的
print("老师 学生 上课 校长 , 有哪个是不匹配的? word2vec结果说是:"+model.doesnt_match("老师 学生 上课 校长".split()))
print("汽车 火车 单车 相机 , 有哪个是不匹配的? word2vec结果说是:"+model.doesnt_match("汽车 火车 单车 相机".split()))
print("大米 白色 蓝色 绿色 红色 , 有哪个是不匹配的? word2vec结果说是:"+model.doesnt_match("大米 白色 蓝色 绿色 红色 ".split()))
#直接查看某个词的向量
print('中国的特征向量是:')
print(model['中国'])效果如下: